В. П. Жарков
Некоторые особенности распределения точек на земной
поверхностиМосква
1999 гВ действительности все выглядит иначе, чем на
самом деле.
Станислав Ежи Лец
Постановка задачи, исходные данные
Целью данной работы является попытка найти возможные закономерности распределения точек на земной поверхности для выделенных регионов с точки зрения некоторых вероятностных функций.
Для рассмотрения выбираются следующие регионы и точки:
Земная поверхность аппроксимируется шаром с радиусом, равным среднему радиусу эллипсоида Красовского ([2] стр.255), что позволяет определять расстояния в выбранных регионах с погрешностью не более 5%.
Координаты точек сняты с [1] с точностью 0.1 градуса.
Все используемые при расчетах формулы приведены в [4],[5],[6] либо легко выводятся с их помощью.
Функции, применяемые в исследовании
Для каждого региона производятся следующие действия:
Первым шагом является построение гистограмм расстояний от каждой точки до всех остальных точек. (Для региона 1 это является повторением работы,приведенной в [3] стр.249 и послужившей толчком к написанию данной статьи. Так как автор проводил все расчеты самостоятельно, это можно считать независимой проверкой). Гистограммы приведены в Приложении 2.
На следующем этапе вводятся дискретные функции T(n,k) и pop(m,n,k), строящиеся следующим образом:
3. Для каждой точки в таблице вычисляется интервал оценки l = Lmax/k, где k задается
как параметр. При проведении расчетов использовались значения k от 2 до 8.
Далее по ф-ле Бернулли определяется вероятность этого события при гипотезе случайного распределения P (popmax).
Вычисляется функция T(n,k)= -lg P (popmax).
Д
ля наглядности эти функции изображаются в виде непрерывных кривых, хотя они,естественно, имеют смысл только в определенных точках.
С помощью функции T(n,k) мы получаем возможность сравнить вероятности реальных распределений точек относительно каждой из них.
При этом следует иметь в виду, что чем меньше значение T(n,k), тем ближе распределение к случайному, чем выше - тем меньше вероятность случайного распределения, то есть правомерно рассмотреть гипотезу о проявлении некоего закона.
Можно предположить, что расположение точек определяется одним или несколькими из 2 объективных факторов и одного субъективного:
- географической конфигурацией региона;
Например, при заселении региона извне (с моря) следует ожидать наибольшего количества точек на побережье, если в центре региона лежит большая слабо заселенная местность (горы, пустыня), точки будут группироваться вокруг нее и т.д.
Некоторые свойства функций Т(n,k) и pop(m,n,k)
Прежде чем приступить к анализу результатов по реальным распределениям, имеет смысл рассмотреть поведение функции Т(n,k) на нескольких вариантах теоретических моделей.
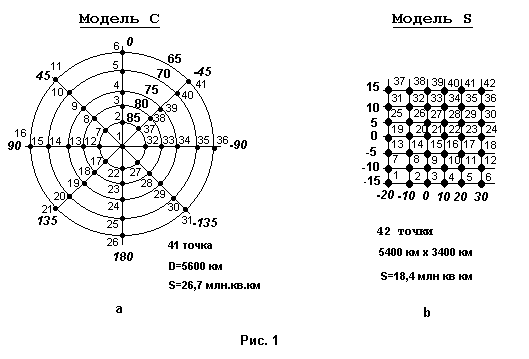
Вариант 1. Распределение точек, показанное на рис.1 (модель с и модель s).
При этом учитывается равенство по порядку количества точек, максимальных расстояний и площади теоретического региона реальным регионам.
Координаты модели смещены на некоторую малую величину, чтобы избежать эффектов, связанных с точными совпадениями.

Поведение Т(n,k) и pop(m,n,k) для модели C и модели S представлено на рис.2 и рис. 3 соответственно. Параметром служит коэффициент деления интервала k=Lmax/l, изменяющийся в интервале 2-8. Для рис. 3 k=4, как дающий наиболее характерный вид.
Дальнейшее увеличение коэффициента ведет к искажениям, связаннным с реальной точностью координат и и “’эффектом невероятного события”–теоретическая вероятность попадания в заданную точку при l=0 l/L=0.
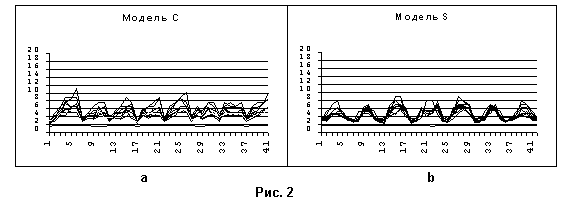
На рис. 2 мы видим, что значения T(n,k) лежат не превышают 12, яркие пики отсутствуют. Рис а показывает, что хотя точки и расположены по окружностям, недостаточное их количество не позволяет выявить их расположение, графики практически похожи. Функция pop(n,k) также имеет “стандартный”, ничем не выделяющийся вид – подъем, максимум, спад с несколькими локальными максимумами, как показано на рис. 3.
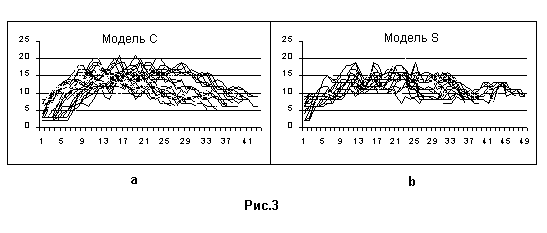
Отметим такое поведение функций как характерное для достаточно равномерного распределения точек.
Вариант 2
: Моделирование проводится с выносом одной из точек за пределы региона. Как показывает анализ, результаты для моделей C и S практически одинаковы, поэтому рассмотрим только первую. В данном случае одна из точек (N 6) удаляется примерно на 1/3 диаметра модели. Как видно из Рис. 4 а удаление точки ведет к яркому увеличению пиковых значений T(n,k), причем как для удаленной точки, так и для некоторых точек региона. На графиках pop(m,n,k) на Рис. 4 b, c, d видно появление сильно отличающейся кривой, это как раз кривая для точки 6 (выделена толщиной). 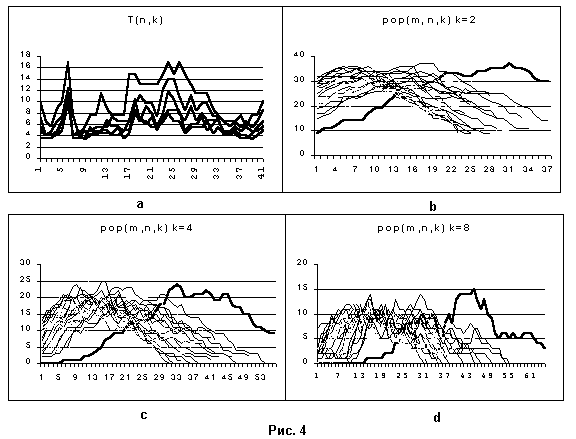
Результат анализа позволяет провести границу между точками региона и точками вне региона (изолированными) по поведению функции pop(m,n,k).
Вариант 4. Рассматривается результат случайного распределения. Выбрана поверхность приблизительно равная поверхности европейско-ближневосточного региона, количество точек 37, координаты выбраны с помощью датчика случайных чисел. Проведено 10 испытаний. Функция T(n,k) для 4 первых для k=2, 4, 6, 8 приведена на Рис. 5, остальные, ввиду их непринципиального отличия, не приводятся.
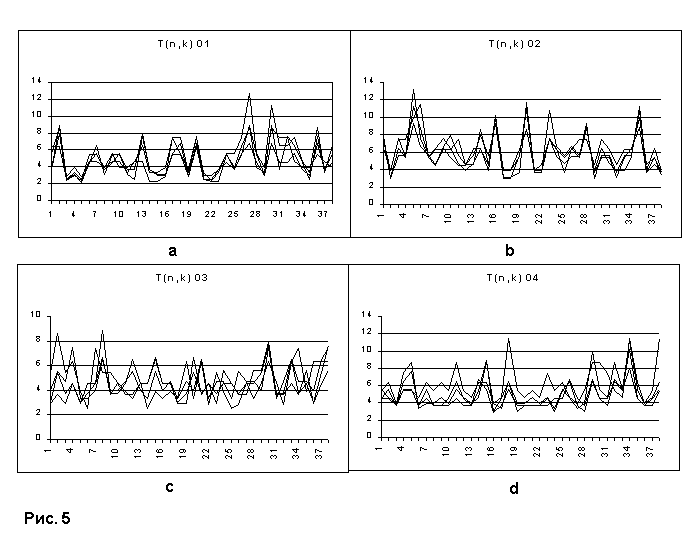
Отметим, что пиковые значения как для равномерных распределений, так и для случайных лежат в диапазоне 8-14, что можно считать для них характерным.
Поведение функции T(n,k) на реальных рапределениях точек
Рассмотрим выбранные регионы в порядке возрастания интереса. Для каждого из них в Приложении 1 приводится 2 графика. Первый – значения T(n,k) при k=2,4,6,8
(кривая для k=4 выделена), второй – суммарное значение T(n) при перечисленных k.
Для удобства графики представлены в виде непрерывных кривых. В приложение 2 сведены гистограммы расстояний для точек рассматриваемых регионов, к которым также может быть полезным обращаться при анализе. Очевидно, максимумам T(n) на гистограммах будут соответствовать участки максимальной длины с наименьшим наклоном.
К сожалению, в Южной Америке (рис.1, 2) на большой территории располагается всего 13 точек, дающих весьма невнятную картину, не позволяющую сделать никаких выводов. Значения T(n,k) ниже значений для случайных распределений.
Набор точек здесь достаточно велик (прил.1 рис 3, 4), однако график близок к графикам случайного распределения. Никаких особенностей не наблюдается.
Графики для Африки (прил1 рис. 5, 6) более выразительны, хотя почти не выходят за пределы случайного распределения. Обратим внимание на максимумы (Триполи, Тунис, Каир). По гистограммам (прил. 2. 3. 15, 38, 39) видно, что “слой ” точек с максимальной плотностью (приблизительно R=3500 км, толщина около 1500 км) для Каира приходится на северо-западный берег континента, а для Триполи и Туниса на северное поберережье Гвинейского залива, это можно увидеть на любой географической карте. Очевидно, что заселение (в смысле строительства населенных пунктов, ставших потом столицами), велось здесь, преимущественно, с моря. Для прочих точек график показывает распределение, близкое к случайному.
В распределении для Соединенных Штатов явно выделяется точка Лансинг (прил.1 рис. 6, 7 и прил. 2.2.18). По карте можно увидеть, что кольцо со средним радиусом около 1000 км и шириной 700 км охватывает Атлантическое побережье и побережье Мексиканского залива, расположенные в виде грубой полуокружности относительно Лансинга. Этот же факт отражается в пиках для Нашвилла, Колумбии, Сент-Пола, Чарльстона.
Далее приступим к рассмотрению наиболее интересного региона в 2 вариантах: только европейские столицы и столицы Европы и Ближнего Востока. Это допустимо, так как Европа и Азия не представляют из себя существенно изолированных образований, и их границы не могли сильно затруднить взаимопроникновение при миграциях.
5. Европа
Рис. 9, 10 Прил.1 резко отличаются от предыдущих наличием ярких пиков. Отметим, что максимальные значения для Лиссабона и Варшавы достигаются при k=2, иными словами, сгущение точек лежит в дальней и ближней половине, соответственно. Это объясняется проявлением эффекта изолированной точки, повышающего значения T(n) не только для самой точки, но и для некоторых центральных точек региона (см. рис. 4). Тем не менее, оставим Лиссабон в выборке.
Гораздо интереснее два пика при k=4. Это Владимир и Москва, естественно, (как отмечено в [3, стр .251]) из-за близости расположения в них проявляются одинаковые закономерности. Значение T(n,4) для Владимира превышает 16 (!). Напомним, что функция T(n,k) логорифмическая, и разница в вероятности по сравнению с ближайшим пиком достигает четырех порядков.
6. Европа и Ближний Восток
В этом регионе, в отличие от выборки в [3 стр.251], автор считает возможным исключить точку Кабул, так как поведение функции pop(m) с полным правом позволяет считать ее изолированной, что отражено на графике этой функции на рис. 6. Предлагаем сравнить его с графиком изолированной точки рис. 4.
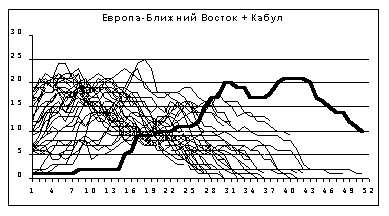
Рис. 6 Кривая для Кабула выделена.
Следовало бы ожидать, что что добавление точек Ближнего Востока, как лежащих в стороне от Европы (а среди них могут быть близкие к изолированным), сильно изменит расположение максимумов. В действительности, результат (Прил. 1 рис. 11, 12) противоположный: максимальное значение для Владимира увеличивается почти до 19, то есть разница с ближайшим пиком составляет уже девять порядков. По поводу максимумов для Лиссабона и Рима справедливо сказанное в п. 5 относительно Лиссабона и Варшавы – Лиссабон так и остался точкой на границе изолированности, а центральная область региона переместилась к юго-востоку (центр тяжести точек первого региона примерно 49°с.ш. 13°в.д., второго - 46°с.ш. 20°в.д.).
Автору не удалось найти объективных причин такого расположения точек этого региона.
Заключение
Из изложенного выше автор считает возможным сделать следующие выводы:
Автор намеревается продолжить рассмотрение данной темы и будет благодарен за замечания и пожелания.
Литература:
1. Под ред. С.И.Сергеевой “Атлас мира” тт 1-4 ГУГиК М. 1981
2. Под ред. Л.Н.Паффенгольца “Геологический словарь” тт 1,2 Недра М. 1973
3. Г.В.Носовский А.Т.Фоменко “Библейская Русь” т 2 Факториал М. 1998
4. М.Я. Выгодский “Справочник по элементарной математике” ГИФМЛ М. 1963
5. Под ред. К.П.Яковлева “Краткий физико-технический справочник” т 1 ГИФМЛ М.1960
6. В.Е.Гмурман “Теория вероятности и мат. статистика” Высшая школа М.1999
vzharkov@emgas.gazprom.ru